The only way to measure the gravitational constant of earth is by observing a falling object. Do not misunderstood by the term falling object. Here are some examples of falling objects – Freely Falling Ball, Satellite, Pendulum, etc.
Here, I will be using a freely falling object to calculate the gravity.The challenge is to find the accurate value of the g constant with both the statistical and systemic errors. In this case, I will be ignoring the effect of air drag. This drag will decrease the g-value.
The basic requirements for this experiment is an Arduino board, a Photogate (or Slotted Optical Switch/Sensor) and a PC with CERN ROOT Package. I will be using almost the same code used in the V-I Advance Example. (But, this time the data is real.) It is not necessary to use ROOT particularly. Anyone can use their preferable package(s) for analyzing the data.
Now, we need a falling object. I am using a thin but steady transparent sheet salvaged from a CD case as the falling body. The sheet is thin enough to pass through the photogate. As the sheet is transparent, the photogate will not respond to its movement. So, I pasted black PVC tape on the sheet in such a way that the sheet has consecutive regions of transparent and black strips on it at a fixed interval of 5mm.
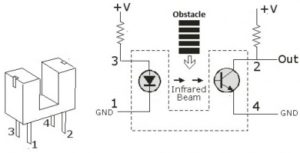
The photogate consists of a IR LED and a photo-transistor. Resistors with values 330 and 47k is used for IR LED and photo-transistor respectively. GND and +V of the photogate is connected to GND and +5V of Arduino respectively. The OUT of photogate is connected to D2 of Arduino.

When the sheet is falling through the photogate, the photogate will change state whenever there is a border of transparent and black strip. This change of state will be recorded in time measurement. So, we have now have the data of the distance covered by the falling object in some certain time. This data can be fit using the famous formula.
s=ut+\frac{1}{2}gt^2 \text{Or, } t=\frac{-u+\sqrt{u^2+2gs}}{2u}To record the data, I wrote a simple piece of code to run a Arduino UNO board. The photogate is attached to the pin D2 (or interrupt pin 0) of the board. The code is given bellow.
Code for Recording Data from Arduino
Every time the sheet falls through the gap, the time readings are displayed on the serial monitor. After each fall, reset the board and follow the same procedure as many times as possible. I repeated for 131 times. The collective data file looks like this.
Now, if you are feeling lazy and could not repeat, then plot the distance VS time data use the V-I Basic Example to fit the data with pol2. This will give you a fair result. I have made a little video on this. It contains only basics of this experiment. Perhaps, you would like to see the video before continuing forward.
But, if you want to get something more, then try to understand the next code.
Code for Analyzing the Gravity Data
In the code, I am calculating the error on both time and distance separately. The calculation of error on time is standard. But the calculation of this thing for the distance is little tricky. Since, the falling object is hand-build by me, the gaps are not uniform. So, I calculated the true positions using the time data. And then calculated the error. Here is the output PS File.
Now, the result may look disappointing. We ended up having a value which is way off the true value with large errors. So, lets point out the facts which we learned from this experiment.
- The velocity of the falling object is too higher to neglect the air drag. That is why wise people use pendulum to measure g-value.
- With increasing time, the velocity of the object increases making the error larger.
- Sometimes the object touched the photogate while falling. But, I did not rejected those samples.
- And finally, the statistical error can be improved by gathering more and more datasets. But the systemic error cannot be improved by this way. This setup can work within a vacuum chamber if the object is falling without touching the photogate.
This experiment is a perfect example to demonstrate the students the systematic and statistical error.