This section, we will learn how to generate a arbitrary distribution from a uniform distribution. Here, we have a random number generator which return a floating point value from the range [0,1] uniformly. We need to generate other distribution (i.e. Gaussian, Poisson etc) from this uniform distribution.
The picture bellow roughly shows the concept of transformation of variables.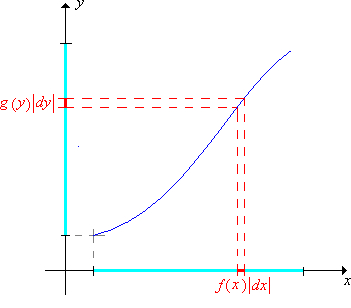 Let say, we can generate the function f(x). And the function g(y) is needed to be generated. Then,
Let say, we can generate the function f(x). And the function g(y) is needed to be generated. Then,
f(x)\left|dx\right| = g(y)\left|dy\right|
Let us consider the radioactive decay. There the functions are f(x) = 1 and g(t) = \frac{1}{\tau} e^{-\frac{t}{\tau}}. So,
\int dx = \int \frac{1}{\tau} e^{-\frac{t}{\tau}}dt + C
\text{Or, } x = -e^{-\frac{t}{\tau}} + C
Now, for x=0, t=0. So, C= 1. Then,
t = -\tau\ln (1-x) \sim -\tau\ln (x)
As x[0,1], \left(1-x\right) \sim x.
I have written a small code to demonstrate this. The code is given bellow.
Code for Transformation of Variables
In this code, I have generated a radiative decay spectrum with decay constant \tau = 5 using a uniform distribution or uniform random number generator. See the plots bellow.
Plots for Transformation of Variables
From the second plot, you can find the slope of the plot as 0.2003 which means the decay constant of the generated distribution is \tau = \frac{1}{0.2003} = 4.9925. This result is consistent with the value we used to generate the plot.
Tags: TRandom, TH1, TPostScript, TMath